Currency Options
Traded both on OTC and the exchange market. Options differ from other derivatives contracts in the idea that it gives the holder the right, not an obligation to exercise the contract. These derivatives are referred to as contingent claims. It is important to distinguish them from other derivatives in the fact that options contracts are more flexible contracts. Because of the nature of option contracts, they tend to be extra complex on computation from other derivatives such as the forwards and futures.
Key Concepts.
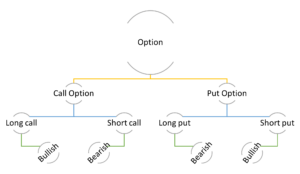
- Buying a call: The right but not obligation to purchase as an asset.
- Selling a call: Writing an option.
- Buying a put: Right not obligation to sell an asset.
- Selling a put: Anticipation that the price will rise and will enjoy the premium.
Terminology in Option contracts
- Exercise: Refers to exercise the rights vested in the option contract.
- Exercise or Strike price: The exchange rate or price at which the long position to the option contract will buy or sell the underlying currency.
- Premium: The upfront payment made by the long position granting them the rights to exercise the option in the future. It can be referred to as the price of the option contract.
- Expiration date: The prescribed date on which the contract will be terminated.
Currency Options: Call and Put
Call options give the buyer the right and not the obligation to purchase the underlying currency at a specified exchange rate. The holder of a call option has the right to buy the underlying currency, while the seller of the call option should sell the underlying currency if and when the holder thereof choose to exercise their right.
A call option is a right to buy a currency at a specified exchange rate, on or before the expiration of the call option contract. The only point to exercise a call option is when the spot exchange rate is above the exercise price. Any point above the strike price is worthwhile exercising the call option because it helps to reduce the loss on the price paid for the premium. This is opposite to the put option, the long position will exercise the option only when the spot price is below the exercise price. The payoffs from the call option can be very high, however, the put option profits go up to point zero, when the spot price approaches zero, the holder has to consider exercise it because the option is tantalizing towards zero (CFA, 2019).
Short position: The short position sells a call option in anticipation that the price will fall (bearish) and the long position will not exercise it. The short position is exposed to considerable risk if the underlying price rises, the loses can accumulate to very large amounts. Hence the premium paid has to well compensate for potential loses.
Interpretation currency options
| Option type
|
The spot exchange rate is greater than the strike price | The spot exchange rate is equal to the strike price | The spot exchange rate is less than the strike price |
| Calls | In-the-money | At-the-money | Out-of-the-money |
| Puts | Out-of-the-money | At-the-money | In-the-money |
Question
A put option allows the holder to sell NOK250 000 at an exercise exchange rate of 0.190 (AUD/NOK). If the premium paid is 0.4 Australian cents for each NOK, calculate the net payoff at the following spot exchange rates:
(a) 0.200
(b) 0.192
(c) 0.180
d) At what exchange rate will the holder break even?
Solution
a) At 0.200 the holder will not exercise the option, losing the premium. The net loss will be:
250 000 x (-0.004) = -1000. Exercising would make the holder lose the following amount:
250 000 x (0.19 – 0.2 – 0.004) = -3500
b) The holder will not exercise, losing the premium. The net loss will be: 250 000 x (-0.004) = -1000. Exercising would make the holder lose the following amount:
250 000 x (0.19 – 0.192 – 0.004) = -1500.
c) At 0.180 the holder will exercise, making net profit of:
250 000 x (0.190 – 0.180 – 0.004) = 1500
The above results a and b are out of the money, c is in the money
d) The break-even spot rate, which produces zero net profit, can be calculated from the following equation:
250 000 x (0.190 – S – 0.004) = 0
Which gives S = 0.1860
At this exchange rate the option is at the money.
Question
A call option allows the holder to buy US$100 000 at an exercise exchange rate of 1.8000 (AUD/US$). If the premium paid is 0.5 Australian cents for each US$, calculate the net payoff at the following spot exchange rates:
(a)1.8040
(b) 1.8260
(c) 1.7870
(d) At what exchange rate will the holder break even?
Solution.
A call option is a right to buy a currency at a specified exchange rate, on or before the expiration of the call option contract. The rationale to exercise a call option is when the spot exchange rate is above the exercise price. Any point above the strike price is worthwhile exercising the call option because it helps to reduce the loss on the price paid for the premium. Though exercising the option will not result in realising a profit it will go a long way reducing the amount lost in the form of premium.
(a) At 1.8040 the holder will exercise, buying the USD at 1.800. By selling spot at 1.8040, the following net loss will be made:
100 000 x (1.8040 – 1.800 – 0.005) = -100
(b) At 1.8260 the holder will also exercise, making the following net profit:
100 x (1.8260 – 1.800 – 0.005) = 2100
(c) At 1.7870 the holder will not exercise, losing the premium. The following net loss will be made:
100 000 x (-0.005) = -500
(d) The break-even spot rate, which produces zero net profit, can be calculated from the following equation:
100 x (S – 1.800 – 0.005) = 0, which gives S = 1.8050.
Interpret the above outcomes (in the money, out of the money, at the money)
Question
A currency dealer is considering trading between Australian dollar (AUD) and Norwegian Krone (NOK) A put option allows the holder to sell NOK400 000 now at an exercise exchange rate of 0.2540 (AUD/NOK) If the premium paid is 0.7 Australian cents for 1each NOK, calculate the net payoff at the following spot exchange rates
| (a) | 0.2410 | [2] |
| (b) | 0.2786 | [2] |
| (c) | 0.1856 | [2] |
| (d) | At what exchange rate will the holder break even? | [2] |
For Put Option (Exercise rate -Spot rate -Premium) X Amount
- ((0.254-0.2410)-0.007)) X NOK400 000 =AUD2400
- ((0.254-0.2786)-0.007)) X NOK400 000=(AUD12,640)
- ((0.254-0.1856)-0.007)) X NOK400 000=AUD24,560
- BEP =Exercise rate – Premium (0.254-0.007) = 0.247
OR
| Exercise Rate | Spot rate | Exercise Decision | Gross Proceeds | Exercise
Value |
Option Premium | Net Proceeds |
| 0.254 | 0.2410 | YES | AUD101 600 | AUD96 400 | AUD2 800 | AUD2 400 |
| 0.254 | 0.2786 | NO | AUD101 600 | AUD111 440 | AUD2 800 | (AUD12 640) |
| 0.254 | 0.1856 | YES | AUD101 600 | AUD74 240 | AUD2 800 | AUD24 560 |
Option outcomes
Bibliography
Hull, J., 2012. Options, futures, and other derivatives – solutions manual, 8. ed., global ed. ed. Pearson Education, Harlow.
Madura, J., 2011. International financial management. South-Western Cengage Learning, Mason (Ohio).
Ritchken, P., Professor, K.W.H., n.d. Futures and Option Markets. 37.
