Question 3
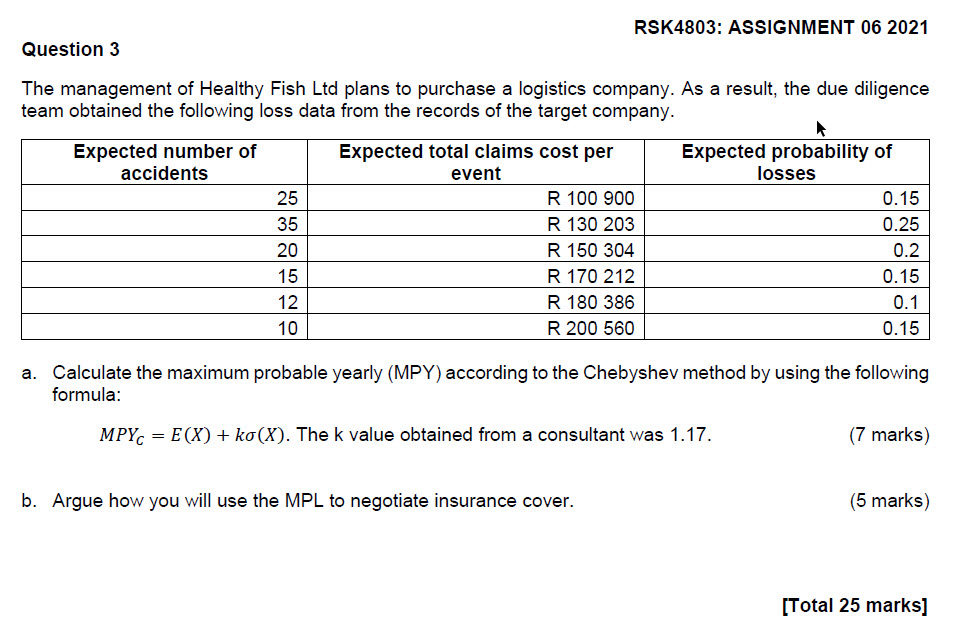
| Expected number of accidents
|
Expected total claims cost per event
|
Expected probability of losses | X Value LOSS |
| 25 | R 100 900 | 0.15 | 25*100 900 = R2 522 500 |
| 35 | R 130 203 | 0.25 | 35*130 203 = R4 557 105 |
| 20 | R 150 304 | 0.2 | 20*150 304 = R3 006 080 |
| 15 | R 170 212 | 0.15 | 15*170 212 = R2 553 180 |
| 12 | R 180 386 | 0.1 | 12*180 386 = R2 164 632 |
| 10 | R 200 560 | 0.15 | 10*200 560 = R2 005 600 |
| P | X | x*P(x) | x-μ | (x-μ)2 | P(x)* (x-μ)2 |
| 0.15 | R2 522 500 | 378 375 | 2 522 500-3 019 147 = -496 647 | 246,658,242,609 | 36,998,736,391 |
| 0.25 | R4 557 105 | 1 139 276 | 4 557 105-3 019 147 = 1 537 958 | 2,365,314,809,764 | 591,328,703,441 |
| 0.2 | R3 006 080 | 601 216 | 3 006 080-3 019 147 = – 13 067 | 170,746,489 | 34,149,298 |
| 0.15 | R2 553 180 | 382 977 | 2 553 180-3 019 147 = – 465 967 | 217,125,245,089 | 32,568,786,763 |
| 0.1 | R2 164 632 | 216 463 | 2 164 632-3 019 147 = – 854 515 | 730,195,885,225 | 73,019,589,522 |
| 0.15 | R2 005 600 | 300 840 | 2 005 600-3 019 147 = – 1 013547 | 1,027,277,521,209 | 154,091,628,181 |
| μ = 3 019 147 | Variance = 888,041,593,596 | ||||
| Standard Deviation = R942 359,59 | |||||
𝑀𝑃𝑌𝐶=𝐸(𝑋)+𝑘𝜎(𝑋)
3 019 147 + 1.17(942 359,59) = R 4,121,708
