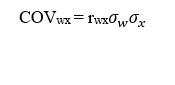Portfolio Standard Deviation

Coefficient of correlation: A standard measure

The coefficient of correlation is derived from the covariance and it helps portfolio managers to compare the interactive risk in a more standardised manner by providing a spectrum between -1 to 1. It is therefore relatively easier to interpret the relationship between securities in a portfolio

Formula for coefficient of correlation 

 

 

 

 

 

 

Therefore, we can rearrange the formula above to obtain the Covariance of security W and X. By making COV_wx the subject of the formula we can deduce the formula equation

 

 

Interpretation of Coefficient of correlation

rwx	-1	0	1
Nature of relationship	Perfect negative correlation	Independent securities	Perfect positive correlation

Variance and Portfolio standard deviation

To understand the risk profile of a portfolio we need to calculate the variance of the portfolio. Variance is the weighted average of the variances of the securities contained within a portfolio.

Variance for a two-asset Portfolio is calculated as

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Example

The following information is available for security W and X.

	Security W	Security X
Weight	30%	70%
Return	10%	15%
	45%	35%
1.        rwx                                   -0.65 2.        rwx                              0 3.        rwx                                    1 4.        rwx                            -1

You are required to you the above information to calculate?

1. Portfolio expected return
2. Portfolio variance
3. Portfolio standard deviation

Diversification: Risk reduction

When securities are combined, we reduced the overall risk associated with a portfolio. By diversification of we can reduce the variance and standard deviation of returns for the overall portfolio without tempering with the portfolio return. Diversifying in several securities decreases the exposure to firm-specific factors, this leads to portfolio volatility continues to decrease. (Kierkegaard et al., 2006).

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

From this calculation, we can deduce that the risk has fallen to 18.78, compared to 45% and 35% of security W and X respectively. Hence, we can conclude that diversification for uncorrelated securities is worthwhile.

According to (Kasilingam, n.d.) The risk and return of a portfolio depends on

1. The risk and return of each security and the covariance of these securities in a portfolio.
2. The percentage of funds allocated to each security.

Bibliography 

1. Kasilingam, D.R., n.d. Reader, Department of Management Studies, Pondicherry University Puducherry 292.
2. Kierkegaard, K., Lejon, C., Persson, J., 2006. Practical Application of Modern Portfolio Theory. JÖNKÖPING UNIVERSITY